Finding the beginning of a loop in a link list.

Let's jump right into it.

I uploaded the drawings I made while trying to understand the algorithm. Just some rough sketches, thought it'd be handy.

4 steps.

Step 1: Assign two pointer to the head of the link list.

Slowpointer-Traverse 1 step at a time

Fastpointer- Traverse 2 steps at a time.

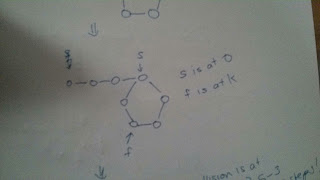
As you see here, both the f and s pointer are at the head of the link list.

Step 2: By the time the slow pointer has entered the loop, the fast pointer will be at k steps into the loop.

As you see here, s is at the beginning of the loop (position 0) and f is at k steps into the loop (3)

Step 3: Now both the pointers will collide at a single location after (length of loop-k) steps

Here the length of the loop is 5. And k was 3. So after traversing the s and f pointers 2 more times with their respective speeds they'll collide at the point show in figure. This point is k steps away from the head of the loop.

Step 4: Move your slow pointer to the head of the link list and start traversing both pointers with a speed of 1. The next time they'll collide, will be at the head of the loop. Ta-da! you're done.

Here, after f and s move 3 more times with a speed of 1, they'll collide at the head of the loop!

Kadane's Algorithm

So kadane's algorithm is to find the maximum sum of continuous numbers in a 1D array (i.e you're finding a subarray).

What's special about this you ask?

Well its complexity is of O(n)

Here's a simple pseudocode.

Kadane’s Algorithm: 
First: max = 0 
max_end = 0 
For each element of the array: 
(a) max_end = max_end + a[i]
(b) if(max_end < 0) max_end = 0 
(c) if(max < max_end) max = max_end return max

So basically we're looking for a list of positive numbers. 

If a negative number appears when max_end==0, we don't need to start counting the sum as the negative number will be less than zero, and we're trying to maximize the sum.

Otherwise if the max_end is greater than max, update the new value of max to max_end. 

Check this example. 
Eg -3,2,4,-3,6 
Firstly -3 appears, so since max_end now equals -3, we make max_end=0. 
Next 2 comes up, so max_end=2 and since max_end>max make max=2. 
Next 4 comes up, so max_end=2+4=6 and since max_end>max make max=6. 
Next -3 comes up, so max_end=6-3=3 and since max_end<max retain max=6. 
Next 6 comes up, so max_end=3+6=9 and since max_end>max make max=9. 
Hence our maximum sum of numbers in the subarray is from i=1 to i=4 which totals upto 9. 

This algorithm can be used in a variety of programming problems.